
Aug. 8, 2018
Settlers of Catan: A Study on the Role of Roll Order
IntroductionOne of the best parts about being a scientist is spending time conversing with other scientists. When I was a graduate student studying in an Experimental and Research Psychology master's program, I lived with other psychology graduate student researchers.
During our free time, which admittedly could be pretty limited, we often relaxed while playing cards or board games. Settlers of Catan, in particular, was a favorite. Despite this occurring during our relaxation hours, our researcher minds wouldn't always turn off when we closed our books or laptops.
While playing Settlers of Catan we started wondering if there were certain variables that predicted outcomes to games. We came up with some basic hypotheses at the dinner table. Consequently, over the course of 10 months, we collected data from our games.
In many ways, the study has been more of a demonstration of experimental confounds and poor methodology than an example of uncovering knowledge through research design (see Discussion section for a list of the many confounding variables). However, we knew this would be the case going into the study.
It was agreed upon that the amount of rigor in data collection that was necessary to create a well-designed study was roughly proportional to the lack of enjoyment we would experience during the process (it was during our free time remember). The issue we faced is a classic problem in science—we had to struggle with the reality of our lack of funs.
Basic Statistics
Before I get into the study, I want to briefly cover the basics of probability as it relates to dice rolls and Settlers of Catan.
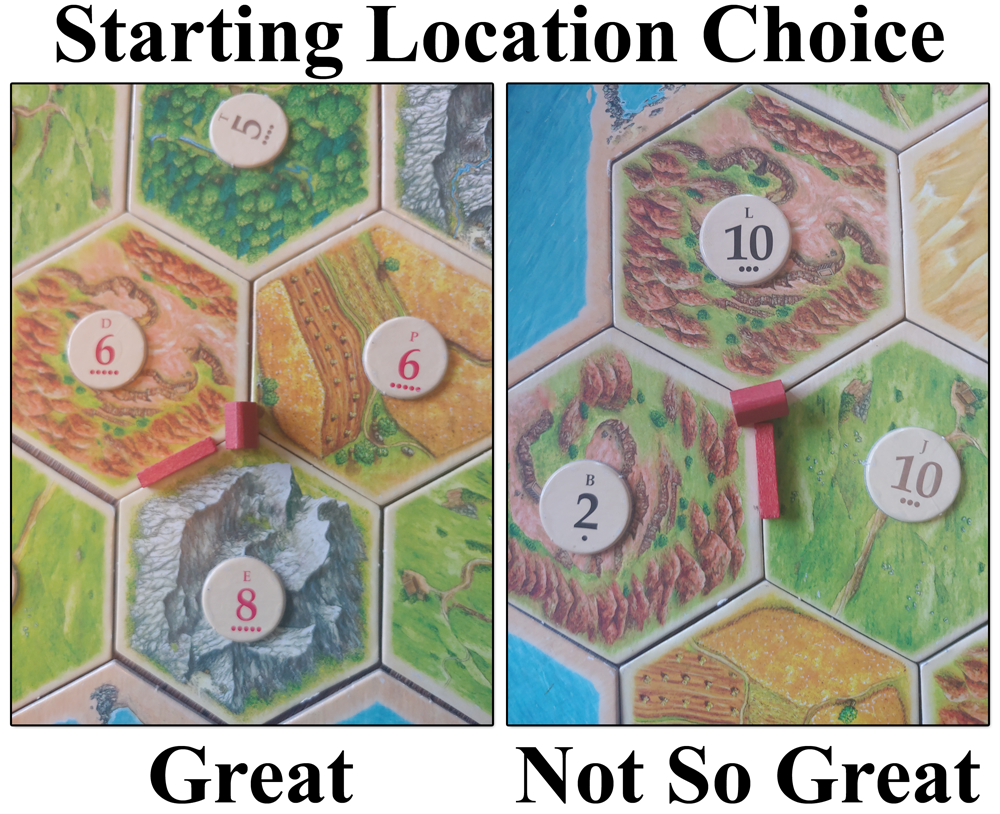
In Settlers of Catan players compete over limited resources in order to advance in the game. Players begin with two settlements and from there can build outward. Settlement locations have different resources that are used to complete various actions in the game (e.g., building roads, new settlements, and purchasing specialty cards–referred to as "development cards"). The resources are brick, lumber, wool, grain, and ore–which are acquired throughout the game with the rolling of two dice.
To begin the game, players do a roll-off to set the roll-order. The player who goes first is given the first pick at setting their initial settlement. Every player does this in order, before the second round of picks begins. This second pass is conducted in reverse order, such that the person who is in the last position for roll order selects both of their first two settlements at once.
When selecting an initial settlement location, there are several factors important to consider. Chief among them are what resources are connected to a location and what number is attached to each resource. All resources have numbers attached to them, which serve to deal out resources to any players with a settlement located there when that number is rolled.
This is where understanding the basics of probability comes into play.
There are 36 possible permutations each time you roll two dice, which have a normally distributed range of values from 2 - 12 when summed. This distribution makes 7 the most likely to be rolled, followed equally by 6 and 8, then 5 and 9, and so on.
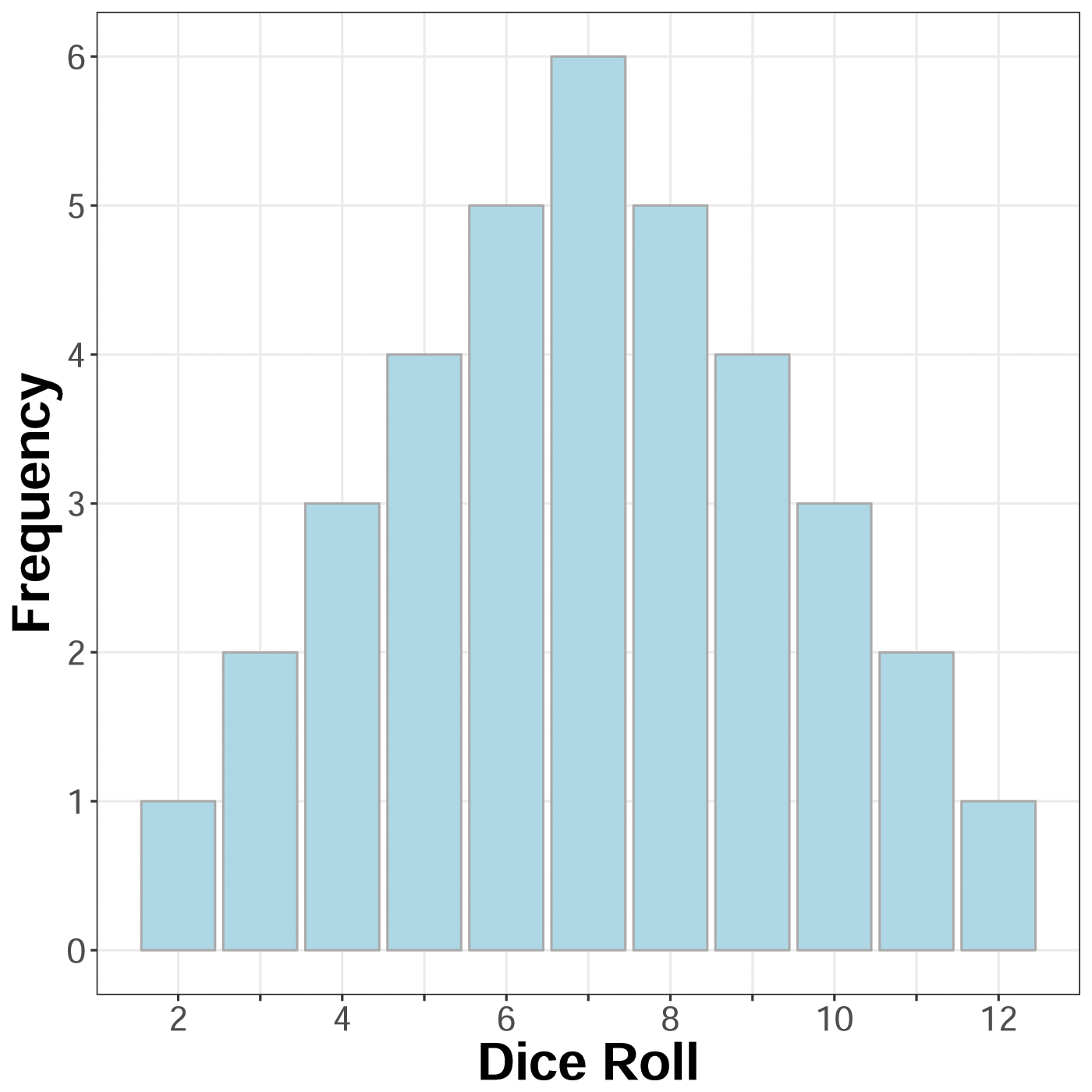
Distribution of dice roll frequencies with two dice.
Setters of Catan uses the roll of a 7 as a specialty roll (known as activating the robber), which allows for the roller to steal a resource card from another player and block a chosen resource on the board from providing resources when its numbered is rolled. Additionally anyone with more than 7 cards has to discard half of their cards. This specialty roll serves as an equalizer in the game. It should come as no surprise that game designers often leverage probability against you. This is how casinos stay in business (and why in the game of Craps, you “crap out” on 7).1
The best locations to pick have 6's or 8's attached to the resources. This is more likely to give a greater yield of resources over time (known as the law of large numbers, where the true probability is met given enough samples). Of course, there are other nuances to consider, for instance, distance from other players and the variety of resources one has access to.
Despite playing the game with individuals who have taken a handful of statistics courses, it was common place in our games to hear things like “fours are better than eights” or “threes are the new fives!” Many other superstitions developed in our games over time as well. When a certain dice roll was hoped for and then subsequently rolled, players would often respond with a whispered, "Jumanji."
The Study
The study originated from noticing that roll order seemed to be related to game outcomes. We began systematically tracking players' roll position and how many points they earned throughout the course of the game (i.e., "Victory Points"), whether a player won or not, and if they held the title of either "Longest Road" or "Largest Army."
Participants
A total of 16 unique players were present in the collected data. Four of the individuals were disproportionately represented in the games played (N = 80) with 72, 70, 68, and 48 games played a piece, compared to the next highest individual who only played in 16 games (some individuals only played one game).
Design
The standard Settlers of Catan game board was used. However, starting at the 30th game, the standard expansion set cards were included in all subsequent games.
During the first 20 games we did not collect data on which player earned the longest road or the largest army.
Players could not earn more than 10 points. If, for example, a player had 9 points and then earned the longest road (worth 2 points), the player would still end with 10 points (the amount needed to win the game).
Victory points from development cards that were possessed but had not been played yet, counted towards total points for a player at the end of a game.
Results
Three player games and four player games were analyzed separately. I didn't include any expansion set games (those with 5 or 6 players).
Three Player Games. The mean victory points for players in games with three players (n = 39) was 7.38 (SD = 2.37). The mean victory point score for individuals who rolled 1st, 2nd, and 3rd was 8.18 (SD = 2.32), 7.05 (SD = 2.43), and 6.92 (SD = 2.23), respectively.

Average victory points earned in three player games by roll order. Error bars represent standard error.
A regression analysis was conducted to determine if there was a relationship between roll order and players' victory points. I found a significant negative relationship between players roll order and the amount of victory points earned in a given game, r = -.22, p = .02. This means that players that rolled earlier in the order tended to earn more victory points than those who rolled later.
However, the regression analysis violates the assumption of independence. Multiple responses from the same person cannot be regarded as independent from each other. In response, I conducted a mixed model linear regression.
Mixed model linear regression has elements of both linear regression and repeated measure analyses. I ran this analysis in R with roll order as my fixed factor and individual players as a random effect. The random effect of individual players can account for individual differences in players performance (presumably players differ in their ability in Settlers of Catan, as in most games).
I found the variable of roll order to be significantly predictive of victory points at the end of a game, χ2 (1) = 7.95, p < .01. Again, supporting the conclusion that those who rolled earlier tended to earn more victory points in three player games.
Next, binary logistic regression was used to identify the effect roll order had on whether or not a player won a game. A significant relationship was found between players’ roll order and games won, χ2 = 7.92, p < .01, Nagelkerke R2 = .10. Like earlier, individuals who rolled first fared better than individuals who rolled later.
I was curious if there was a relationship between roll order and earning the longest road or the largest army. The variables were coded dichotomously for having the longest road or largest army at the end of the game (yes vs. no).
Interestingly, a binary logistic regression demonstrated a significant relationship between roll order and earning the longest road, χ2 = 3.90, p = .048, Nagelkerke R2 = .07. Individuals who rolled first were more likely to earn the longest road than the latter rollers.
No significant relationship was found between roll order and earning the largest army.
Four Player Games. The mean victory points for players in four player games (n = 35) was 7.00 (SD = 2.25). The mean victory point score for individuals who rolled 1st, 2nd, 3rd, and 4th was 7.46 (SD =2.36), 6.86 (SD = 2.23), 7.09 (SD = 2.02), and 6.60 (SD = 2.39), respectively.
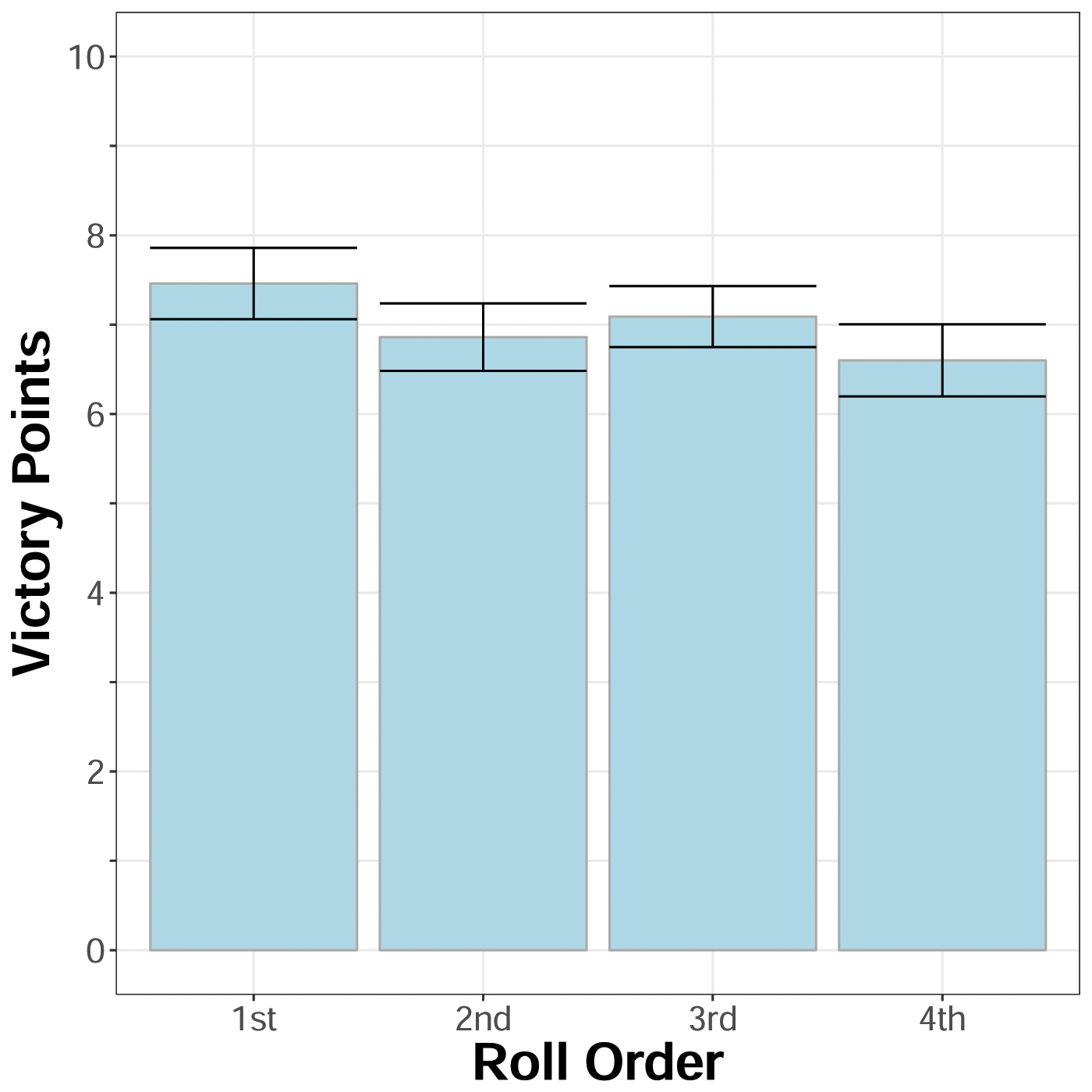
Average victory points earned in four player games by roll order. Error bars represent standard error.
I ran a regression analysis to determine if there was a relationship between roll order and players victory points. There was no significant relationship found between roll order and victory points earned for four player games, r = .12, p = .17. Players were not more likely to earn a greater number of points based on starting roll position.
Again, binary logistic regression was used to identify the effect roll order had on whether or not a player won a game. No significant relationship was found between players’ roll order and games won, χ2 = .62, p = .43, Nagelkerke R2 = .01. Unlike three player games, individuals were not more likely to win games based on roll order in four player games.
In evaluating the role roll order played in four player games for earning the longest road and largest army, two binary logistic regression analyses were run. There was no relationship found for either outcome based on roll order for four player games.
Discussion
I found that in three player games, individuals who went earlier in the roll order were more likely to earn more victory points, to win, and to get the longest road. In four player games, roll order was not successful in predicting outcomes.
I propose that in three player games the reason why the person who rolls first is more likely to earn the longest road may be for two reasons. The first is the importance of road building to create additional settlements may influence early selections to include brick and lumber. Additionally, you are likely picking a solid spot with good numbers (e.g., 6’s & 8’s) and are surrounded by good resources (e.g., brick & lumber). In response to this, the following choices from the opponents may be trying to get in on that sweet hexagonal resource action, creating a compacted area of settlements. The first roller then may have to travel further to place new settlements, thus creating scenarios where earning the longest road is more likely.
One of the factors we didn't measure but I think is important is how concentrated the good numbers/resources are. I believe that in situations where the 6's and 8's are on top of each other (versus spread out across the board) it is better to go first. When the quality starting locations are spread out across the board, it's better to go last in the roll order. I also think this is especially true in three player games, where going last has fewer rollers in front of you (and hence more quality spots left).
It would be interesting to conduct a follow-up study,2 with less confounding variables, that also had a measure of quality starting location concentration. Having the players rate how concentrated versus spread out the quality locations were prior to starting the game could be a simple way of doing this. These ratings could be averaged and used as a covariate in roll order's predictions of game outcomes.
(Oh so many) Limitations. Our roll-off procedure was whoever rolled the highest number went first and then we just went clockwise around the table for the roll order. This decision became more problematic given that players often sat in the same seats, further creating systematic bias.
Once the expansion set was purchased, the numbers placed on the resources and the resources themselves were not always held constant. This means that the probabilities for rolls and resource pay-outs varied across games.
It was not uncommon to have beers and cocktails during games. Intoxication levels varied across games (and players).
Players who lived in the house where games were most often played were overrepresented compared to guests who participated in the study.
Carryover effects were sometimes present. Grudges and informal alliances occasionally formed in response to previous games. For example: "So-and-so can't win again."
Occasionally someone would setup the Settlers of Catan board and wait for others to be ready to play, giving them much more time to study the board and have strategic forethought. This may have resulted in uncontrolled strategy differences (and shouting of "What's taking so long?").
Footnotes:
1 Although statistics struggles to account for how fun it is to throw chips down on the table before a Craps roll while shouting "snake-eyes!"
2 Warning: the active pursuit of quantifying activities during one's free time may result in lower levels of general enjoyment and making guests feel "put off."